Friday, July 27, 2007
Math Around the World
Choose a country and describe in your own words the mathematics people did in that country in ancient times.
Silverio Triangle


Vicky and me created a triangle on cardboard. First we had to draw the triangle on patty paper and then bisect the angles. Then we traced the triangle into the cardboard and we label the vertex and the midpoint. We colored the triangle then we had to balance the triangle in a pencil.
muting's goals
During this summer, I think I improve a lot, before I think I can't wake up to school, but I wasn't late in school. I do all my homework and turn in on time. I think I will keep doing my homework and have a good grade on it, if I don't know how to do my homework, I should ask my teacher and get help. I think I also have to pay more attention to what the teacher say.
Janet's Goals
During this summer, I think I improved alot. I have a goal for the new school year. I want to wake up early in the morning so I won't be late for school and pay attention in class, so I know how to do the work.
Susan's Goals
For this summer program to be over. I learned many things mostly math that I don't know like geometry. It was hard but i learned it little by little and also the academy let me see many colleges and university campuses. It also let me know what are the requirements for colleges and university and that i know what i have to do to get to my goal that is a career in medical. Also I know which classes i have to take to pass high school and also pass the requirements of the university that i want to go. so this is what i learned in the 1st annual summer algebra academy at oakland high school in the summer of 2007 from June 25 to July 27.
MY GOALS
This summer I feel like I improve alot in diffrent stuff because Geometry was new to me. But I still little bit of help in diffrent stuff
Jenny's Goals
During this summer, I think i have improve everything cause i know that i can not be perfect. Also i learned many new things from Ms. Abernethy. THANK YOU VERY MUCH. Basically I really wants to be a doctor, so I needs to do well at school. To reach my dream goals, I needs to be sucessful at SCHOOL. However I still got more school to go, I needs to try my best to achieved my goal. THANK YOU
My Fruity Goal Blog
What I improved on during this Geometry Summer Academy at Oakland High, is doing my home work. I really didn't do my home work a few days in a row, but I improved my home work habits. My ultimate goal is improve my study habits.
Jon's Goals
During this summer Academy I feel like I have gotten better at math and learned how to do geometry. I feel like I have gotten better at paying attention to the teacher and learning to do the assignments. For the future I don't really know what I want to do. Hopefully during high school I know what I want to do and figure out what college will help me achieve my goal.
Vicky`s Goal
This summer, I felt like I improved in doing my homework and not getting lazy about it. My goal for the year to come to school everyday and be on time.
alex's goals
the things that i learned/improved on is actually coming to class being on time and trying to do my best even though I did not.
But what i really did take with me is better organization skills.
But what i really did take with me is better organization skills.
Centroid
Drew the triangle and found the centroid on the patty paper and then copy the construction on the cardboard. Drew the midpoint and connect it to the vertex. When balance on the pencil it is the median. Measure the length divided by the longer line and get a proportion and it come to a shorter length.
Babylonians Math


Babylonians used clay tablets to do math in them. The clay tablets included fractions, algebra, quadratic and cubic equations. It also had the Pythagorean theorem, and the calculation of Pythagorean triples. Also the Babylonian tablet gives an aproximation to the square root of 2 to 6 decimal places. The Babylonian mathematical system was sexagesimal. Babylonian mathematicians also developed algebraic methods of solving equations. The Babylonians also used geometry and trigonomaetry.
alex's centeriod
the centeriod of the triangle is the point of intersection of the three mediansthe one that I made is balanced directly in the middle. (picture in progress) so as if you divided the tringle in half length wise it would be equal on both sides .
Tuesday, July 24, 2007
Math in China, by Muting
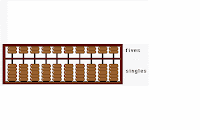


Do you want to know more about the math in ancient china? Let me tell you some, there's a lot a math that the ancient Chinese use, the scales, the abacus and even some of the numbers that the ancient Chinese use. Abacus is one of them, you think the calculator is more easy than an abacus, but when you learn it, it is easy. The abacus have the top and bottom, each circle on top represent 5, and each circle at the bottom represent 1, so at the bottom when you use the thumb move up 1 that means 1, but at the top, when you use the middle finger move down 1, that means 5. That's how the Chinese use the abacus for hundreds ago. The ancient Chinese also use the easy symbol to calculate the math, for example, they place the zero, in to space, so it is easy to remember like the picture that show. They also use the negative numbers, they use it at the last of the number and cross it out so it means negative.
Euclid's Element by Susan L.



Euclid's Elements is a mathematical and geometric treatise, consisting of 13 books, written by the Hellenistic mathematician Euclid in Alexandria circa 300 BC. It comprises a collection of definitions, postulates also called axiom, propositions, and mathematical proofs of the propositions. The 13 books cover Euclidean geometry and the ancient Greek version of elementary number theory. The Elements is the oldest extant axiomatic deductive treatment of mathematics, and has proven instrumental in the development of logic and modern science. Euclid's Elements is the most successful textbook ever written. It was one of the very first works to be printed after the printing press was invented, and is second only to the Bible in number of editions published. It was used as the basic text on geometry throughout the Western world for about 2,000 years. For centuries, when the quadrivium was included in the curriculum of all university students, knowledge of at least part of Euclid's Elements was required of all students. Not until the 20th century did it cease to be considered something all educated people had read.
Jenny's Mayan Number at Ancient Mexico
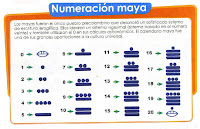

Do you know that Mexico used ancient math? The Maya is an acient tribe in Mexico. The Mayan system of writing numbers was very simple. The way they wrote out numbers was using bars and dots. Each dot represents a 1 and each bar represents a 5. They could used the same system and also they could write out any number from one to twenty by placing bars and dots on top of eachother. There is another way that we could used it, by add two of the Mayan numverals together very easily by adding the dot together. The Mayan system was similar like we are having symbols right now.This same system are also used today in the tribes suchas Hopi and Inuits. They can also add with these large number easily because it mostly be small digits. This is the way that you guys could figure out the Mayan number. First add together the bars and dots in the 1s place. When the sum is over twenty, there will be some carrying to the next will involved. Next, you add the bars and dots in together that are in the 20s place. However, they could used other materials to helps you figure out. Also in the acient time, they used to trade with he same amount of things so they wont get ripped off. Eventually, every country math started to spread over the world and people are started learning and it is alsoo really useful over the world.
Prime numbers



Eucild was the first to prove that prime number is infinity because it goes on forever and ever. He used the well known prime number to add it to every product. For example, 2*3+1=7. Then he continue by adding 5 to the same problem, 2*3+5+1=31 and it came out to be a prime number too. Unfortunally some of the problem didn't come out to be a prime number but there are still more prime when he keep doing the process. This is his proof:P1,P2,P3,..Pn representing the prime and the numbers. Multiply them and then add by 1 calling this a new interger q. When hte multipy and add to equal to q it is a prime number. When the answer is not q then it have to be divided by and it's called r. Dividing q with the prime number will come to a remainder 1 so it can not be a prime number.
Fruity Mathematics used by Ancient Muslims
In this paragraph I'll be talking about how the ancient life of Muslims used mathematics, especially trigonometry.
Trigonometry is also mostly a Muslim creation. It is a branch of mathematics which studies plane and spherical triangles. It developed from the need of astronomers to map points in the sky on a heavenly sphere. Trigonometry's functions, involving ratios such as sine and cosine, tangent and cotangent, were greatly developed and refined in the Islamic lands.
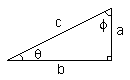
Arab contributions:
Al-Tusi, a Muslim, is the "father of trigonometry".
The idea of trigonometry was originally from the Greeks, by Hipparchus in 140 BCE.
The Muslims further developed trigonometry from their work in astronomy.
Today astronomers use trigonometry for calculating distances to stars, and for measuring distances and heights of buildings, trees, etc.
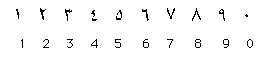
Top: Western Arabic or Hindu-Arabic Numerals

Below: Modern Arabic numerals which developed from them
[ Still Under Construction ]

Trigonometry is also mostly a Muslim creation. It is a branch of mathematics which studies plane and spherical triangles. It developed from the need of astronomers to map points in the sky on a heavenly sphere. Trigonometry's functions, involving ratios such as sine and cosine, tangent and cotangent, were greatly developed and refined in the Islamic lands.

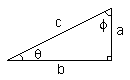
Arab contributions:
Al-Tusi, a Muslim, is the "father of trigonometry".
The idea of trigonometry was originally from the Greeks, by Hipparchus in 140 BCE.
The Muslims further developed trigonometry from their work in astronomy.
Today astronomers use trigonometry for calculating distances to stars, and for measuring distances and heights of buildings, trees, etc.
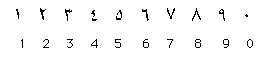
Top: Western Arabic or Hindu-Arabic Numerals

Below: Modern Arabic numerals which developed from them
[ Still Under Construction ]
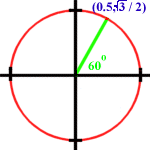
Vicky`s Blog 8
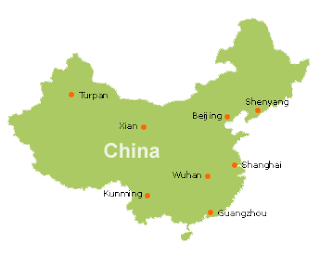
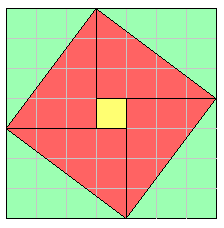

In this blog, we are supposed to pick a country and talk about their history development in math. China was the country who proved that the Pythagorean theorem or the right-angle triangle theory was true. The theory stated that if you add the squares of the legs of the right angle, it is equal to the squares of the hypotenuse (the longest leg). A mathematician name Chou Pei proved it using the picture on the left known as chi-chu. It means the piliing up of squares. China used it as a way to solve algebraic equations using geometry. The picture on the right is a diagram by Zhou Bi. There are four 3 by 4 rectangles around a 1 by 1 square. The four triangles make a tilted square. This was also used to solve the pythagorean theorem.
Jon's Country of Math
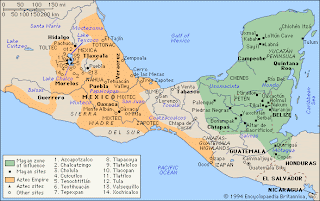

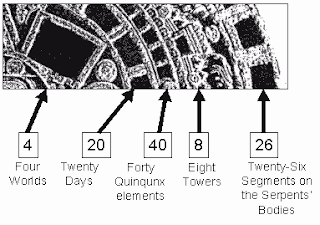
The Ancient Aztec Calender has many different designs to tell the month, the day, and the year. The top rectangular shaped elemnets represent 13Acatl orThirteen Reed. They say that it represents the date upon which the Aztec Calender was made. They started to times all the numbers that represent the shapes together. 4 x 29 x 49 x 8 x 26 = 665600 after they got that number they used the Maya Companion number to get the number 1366560. The one thing that remains to be computed is the 13 Acatl number but someone would already visualize the symbolic math of the 1366560 day count number on the Aztec Calender.
Janet's Calender in China



Did you know that China had a calender? The chinese calendar represents the longest unbroken sequence of time. Time measurement, recording, and prediction of events were the development of the calender and early math. The chinese calendar started around the year 2953 B.C. The chinese calendar is based on the lunar cycle and we still use it today. The chinese calender spread all the way to Japan and Korea. The chinese calender was considered a sacred document. The zodiac has twelve branches and is based on a 360 degree circle. The year is divided into 24 periods. There is also tweleve different animals in the chinese zodiac.
Monday, July 23, 2007
muting's centroid


this are the pictures of centroid that i make with Janet in July 20, 2007. first we have to draw a scalene triangle on a patty paper, to draw a centroid we have to find out the medians and the midpoints, not the vertex, so we can find the centroid. then we copy it down on a cardboard and cut the triangle out. next we place the centroid on a pencil eraser tip and try to balance it. when we see it balance because of the center of gravity make it balance. next we place the centroid on the length of the pencil. this one we have to place it with the longer median, not the shorter median, but this one we have to use some of proportion because it is hard to balance.
Silverio's Fibonacci Numbers


The red and the blue lines show sets of spirals.
Fibonacci numbers are a sequence where the first two terms are both 1. Fibonnaci numbers came from Arabia. We use this numbers in math. Fibonacci numbers are also found in nature. They are found in apples too. The Golden Ratio is much harder. Ancient Greeks thought a most appealing rectangle was one with the proportion of width/length=length/length+width.
Jenea's Fruity Paragraph About 3.5 Centroid Steps 9-11


Here is another real life example of a centroid triangle I made with Jonathan. This second picture of the centroid triangle, we used a wooden pencil to balance the triangle vertically.
Here are real life examples of a centroid triangle I made with one of my friends Jonathan. The first picture of the centroid Jonathan and I made, we used a regular wooden pencil to balance the triangle horizontally.
[Still Under Constrcution)
Fibonacci

http://www.mcs.surrey.ac.uk/personal/r.knott/fibonacci/fibnat.html#bees

http://www.mcs.surrey.ac.uk/personal/r.knott/fibonacci/fibnat.html#bees

http://www.mcs.surrey.ac.uk/personal/r.knott/fibonacci/fibnat.html#seeds
http://www.mcs.surrey.ac.uk/personal/r.knott/fibonacci/fibnat.html#leaf
Fibonacci numbers are sequence that start with a number of term and it creates the value of term. You can use the formula F(n).For example: 1+1=2, 2+1=3, 3+2=5..etc. To solve a rectangle you use width/lenght equal to lenght/lenght+width and then you use proportion which is cross multiplying and then use the quadratic formula.Approximate the 3decimal is called Golden ratio.
darynell's centroid triangle
centroid is considered the center of gravity because it is the one place where a polygon is perfectly balanced meaning it will always be stable at that point as long as both sides remain equal.The centroid goes from the vertex to the midpoint on the opposite side.once all of the lines are established they form the median.When the medians are formed to check your work measure one of the line segments the larger part shold be double the size of the smaller one.
Janet's Centroid


Here are pictures of the centroids that I made with Muting. The centroid balanced on the centroid and the median. Centroid is considered the center of gravity because it will balance and it will not fall. We had to line up the midpoint and the vertix to see if it will balance on the length of the pencil. We had to balance the pencil on the longer median, and not the shorter one. When we had to balance the median on the length of the pencil, we had to use proportion because it was hard to balance it.
Jenny's Centroid Triangle


Here is a picture of a cardboard triangle and it is also being balanced of a pencil. On July 20, 2007, I worked with Susan L. Before we started on the cardboard triangle, we draw a picture on the patty paper. To figure out the centroid of the triangle on the patty paper, we fold each corner to the vertex. After we fold all the 3 angles, there is a place where it intersected which called a median. Then you make an angle bisector to the midpoint to all the 3 triangle to find out the centroid. Also you should trace the patty paper by marking the points on the cardboard. Then you connects every points which should look exactly the same thing. However you wants to figure out the shortest and longest distance you needs to figure out the lengths of each segments. You needs to do the shortest over the longest distance for each segment. The proportion tells the golden ratio of the triangle. All the segments should be the same fraction. Then we used a pencil to balanced it. When we figure out our segment it was one half. It was also really fun that we could decorated and we label it.
Vicky`s Centroid Triangle


On Friday, me and Silverio made a triangle. We started drawing it on patty paper and bisected each angle. Then we marked the midpoint and vertex onto the cardboard and re-drew the triangle. We labeled the center where all three lines intersect the centroid or center of gravity. Then we tried to balance the cardboard triangle on a pencil. That is called the median. You measure the length and make a proportion. It becomes the shorter line / the longer line.
Jon's Centroid Triangle


The centroid triangle we made was able to balance on the median and centroid. We had to put the pencil to aline with the midpoint, median, and vertex. The reason why the triangle balances on the pencil is because of the center of gravity. The length of the shorter segment is 2 times smalller than the longer segment. We need the proportion to help find how many times does the shorter part of the median fits into the longer part of the median.
Subscribe to:
Posts (Atom)


